Parallel Binary Tree Search

Hello there! This article will discuss a Parallel Binary Tree Search tree version using CUDA and OpenMP, explaining the basic idea and how to implement it. Let’s start introducing the tools we use:

OpenMP (Open Multi-Processing) is an application programming interface (API) that supports multi-platform shared memory multiprocessing programming in C, C++, and Fortran. It allows developers to write parallel code easily by using compiler directives, library routines, and environment variables.
CUDA (Compute Unified Device Architecture) is a parallel computing platform and programming model developed by NVIDIA. It allows developers to leverage the power of NVIDIA GPUs (Graphics Processing Units) for general-purpose computing (GPGPU). With CUDA, developers can write programs that run on the GPU, taking advantage of its massive parallel processing capabilities to perform complex computations much faster than on a traditional CPU.

The idea

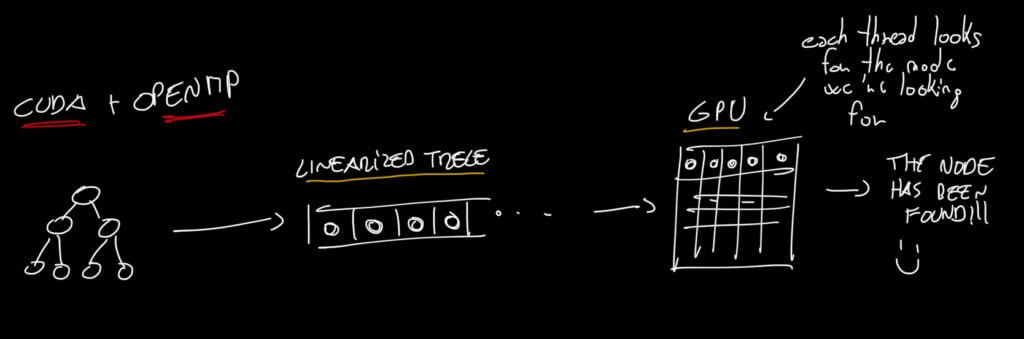
Before discussing the Parallel Binary Tree Search, we need first to understand what’s the idea behind this. As you can see in my beautiful and extremely expressive diagram, in the first step, we use OpenMP to linearize the binary tree in a simple array (we extract the single node from the tree, and then put it in an array).

In the next step, the array is passed to CUDA, where each thread will search for the node with the key we are looking for.

Code

Let’s talk now about the code. In this section, I will show you the most important functions that i used and that basically define the behavior that i explained with the sketch.

inOrder

During execution, the inOrder function visits each node of the tree iteratively with stack in the given implementation ( you can find the implementation i used here), and adds each node to the nodesArray array in the order in which they are visited.

currentIndex acts as a dynamic indicator of the current position in the nodesArray array while the tree is being converted to an array, making it easier to insert the tree nodes into the array in an orderly manner. I used it because it helped me a lot during the funniest part of coding (debug time), so I left it in the code.

        void inOrder(struct Node* root, struct Node *nodesArray, int* currentIndex)
        {
            // Set current to the root of the binary tree
            struct Node* current = root;
           
            // Initialize stack s
            struct sNode* s = NULL;
            bool done = 0;
         
            while (!done) {
                 
                // Reach the leftmost node of the current node
                if (current != NULL) {
                     
                    // Place the pointer to a tree node in the stack
                    // before traversing the left subtree of the node
                    push(&s, current);
                    current = current->left;
                }
         
                // Backtrack from empty subtree and visit the
                // Node at the top of the stack, but if
                // the stack is empty, you're done
                else {
                    if (!isEmpty(s)) {
                        current = pop(&s);
                        nodesArray[*currentIndex] = *current; // Add element to the array that will contain all nodes of the tree
                        (*currentIndex)++;
         
                        // we have visited the node and its left subtree
                        // now we need to visit the right subtree
                        current = current->right;
                    }
                    else
                        done = 1;
                }
            }
        }

Code Copied!

Let’s explain the parameters:

root: It is a pointer to the root of the tree you want to perform in-order traversal.
nodesArray: It is an array of type struct Node* where the nodes visited during the in-order traversal are stored.
currentIndex: Is a pointer to an integer that keeps track of the current position in the nodesArray array. It is updated during the traversal to indicate the next free position in the array to insert the next visited node.

If you want to understand more about how the function works, you can see here a similar implementation which clearly explains all the logic behind this

cudaSearch

This part represents the core of the code. Without that, the Parallel Binary Tree Search doesn’t exist and this article would be just a dream (would say a nightmare). The kernel executes each thread to search for the chosen key. Each thread compares the node to search and the array element which is also a node, if the thread finds the node at index x, it will write in x the value ‘1’ to data_array on the same index, ‘0’ otherwise.

        __global__ void cuda_search(struct Node *data_array, int *result, int num_nodes) {
            int index = threadIdx.x + blockIdx.x * blockDim.x;
        
            if (index < num_nodes) {
                struct Node *p = &data_array[index];
                
                // Comparing current node and node with key we're looking for
                int cmp_result = (p->key == d_searched_node.key) ? 1 : 0;
                result[index] = cmp_result;
            }
        }

Code Copied!

Let’s explain the parameters :

data_array: It is an array of type struct Node* containing the nodes of the tree to perform the search.
result: It is an array of integers that is populated with the results of comparisons between the nodes in data_array and d_searched_node. A value of 1 in result[i] indicates a match between data_array[i] and d_searched_node.
num_nodes: It is the total number of nodes present in data_array (and therefore of the tree).

getNodesByResult

The following function traverses the h_result array to find the first match (value 1). When it finds a match, it returns a pointer to the matching node in the nodesArray. This node represents the tree node that was searched for and found.

struct Node* getNodesByResult(struct Node *nodesArray, int *h_result, int num_of_nodes) {
    struct Node* finded_node = NULL; // Initialize node to return
    
    #pragma omp parallel // Parallelize to check the array with the results containing the matches faster
    {
        #pragma omp for
        for (int i = 0; i < num_of_nodes; i++) {
            if (h_result[i] == 1) {
                finded_node = &nodesArray[i];
            }
        }
    }
    return finded_node; // If you have not found the node, return an empty node
}

Code Copied!

Let’s explain the parameters (last time i explain parameters i swear):

nodesArray: same as before.
h_result: It is an array of integers that contains the results of comparisons between a searched node and the nodes in nodesArray. A value of 1 in h_result[i] indicates that the nodesArray[i] node was found as a match. It is the result array of the previous function.
num_of_nodes: It is the total number of nodes present in nodesArray.

Performance

Let’s talk now about the most interesting part of the article: Performance (not my sketches). We will consider performance in varying parameters (“Numero Threads” is “Number of Threads” in Italian). The measurements have been done in two cases:

By using integer keys (instant compare).
By using much “computationally challenging” alphanumeric keys that take longer to compare.

Note: I compared the results using the different optimization levels provided by the C compiler, and the optimization level that in this case gave the best results was ‘O2‘. They were also used: BlockSize: 1024 and GridSize: ((num_of_nodes – 1) / blockSize.x + 1).

Environment

We couldn’t talk about performance without first mentioning the environment in which the measurements were taken. In this experiment, i have used Google Colab with the following characteristics at the time the measurements were taken.

Specifically, we have Tesla T4 GPU:

Case1: Integer keys

Let’s start by analyzing the performance of our algorithm with integer keys as the number of nodes varies.

We noticed how in general, as the number of nodes increased we went from having speedups that are not particularly appreciable, with some worthy of note. This is because as the nodes increase, and by widening the “thread blanket“, we can cover more nodes in less time. We therefore expect that as the number of nodes increases, we will have times increasingly efficient node search.

Note: for reasons of equality, in both cases a node was chosen that was “in the middle” of the tree.

Case 2: Alphanumeric keys

Now we will consider the case in which the key comparison operation is not a comparison between integers (which is therefore immediate), but that the keys must undergo a particular type of checks which leads to additional time in case key to be found and node current do not coincide, therefore leading to having to move around the tree and having to carry out further comparisons.

In general, the “classical” binary tree searches have a time complexity of O(log(n)), while ours is significantly more since we perform more operations. However, we can see a noticeable performance difference when comparing non-immediate keys and a high number of nodes. It suggests that this approach may be beneficial when we have this type of “challenging key”.

Implementation choices

In our Parallel Binary Tree Search, I’ve chosen to use an in-order traversal method stack-based to visit the tree. This method is more memory-efficient compared to the more commonly used recursive version, especially when dealing with large data structures. Recursion can lead to exceeding the depth limit of called functions, which could happen in our case. In our measurements, we reached one million nodes, but it would be possible to go even further and risk breaking the code due to not enough stack memory allocated to recursive calls. Finally, we note that for the CUDA version, in addition to the use of global memory, it is been used the constant memory type for saving the node to search as this data is the same for all threads and therefore taking advantage of constant memory provided us with further performance advantages.

So, CUDA programming is a tool that proves to be very useful when in our task we need a horde of virtualized (fortunately) zombies that must carry out the same task with different parameters. This is clear proof that having a GPU is fun and that they sell like hotcakes because everyone desperately wants to program with CUDA and maybe play video games.